DERIVADAS LATERALES

La derivada lateral por la izquierda de una función y=f(x) en el punto x=a es el límite de las tasas de variación media TVM[a,a+h] cuando h tiende a cero por la izquierda del cero, es decir tomando sólo valores negativos. Cuando el límite existe y es finito, decimos que la función tiene derivada lateral por la izquierda y es :

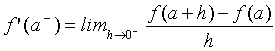
La derivada lateral por la derecha de una función y=f(x) en el punto x=a es el límite de las tasas de variación media, TVN[a,a+h] cuando h tiende a cero por la derecha del cero, es decir, tomando sólo valores positivos. Cuando el límite existe y es finito, decimos que la función tiene derivada lateral por la derecha y es:

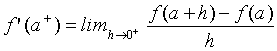
Si en un punto x=a, las derivadas laterales no coinciden, es decir, son distintas, la función no es derivable en el punto x=a.

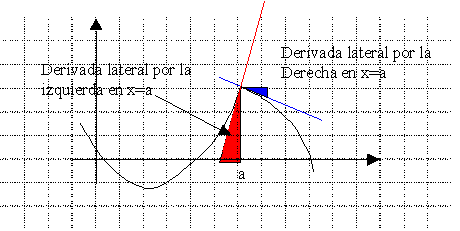
Si la función tiene derivada en un punto x=a, existen las derivadas laterales y son iguales: