representación gráfica
La representación gráfica de funciones puede ser una herramienta útil para la resolución de ecuaciones, no tanto para no conocer el valor exacto de las soluciones, como para saber cuántas de ellas son reales e incluso para acotar sus valores. En el caso más sencillo de una ecuación lineal tendríamos que la ecuación x - 3 = 0 se convierte en una función sin más que poner f (x) = x - 3, que es la ecuación de una recta. El punto donde dicha recta corta el eje X es precisamente la solución de la ecuación, es decir x = 3
De manera que siempre que podamos representar gráficamente una ecuación, las soluciones de la misma vendrán dadas por los puntos en los que ésta corte al eje de abscisas. Por ejemplo, si representamos la función f (x) = x3 + x2 + x + 1 vemos que sólo corta a dicho eje en un punto, concretamente en x = -1, que es la solución a la ecuación x3 + x2 + x + 1 = 0. Como no hay mas cortes con ese eje podemos afirmar que la ecuación tiene una única solución.
Así vamos a estudiar un tipo de ecuaciones, para ejemplificar lo anterior:
Gráfica de las funciones cuadráticas
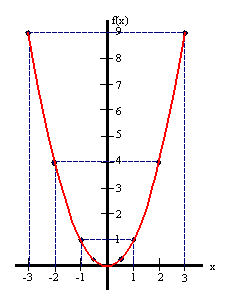
La función cuadrática más sencilla es f(x) = x2 cuya gráfica es:
| x | -3 | -2 | -1 | -0'5 | 0 | 0'5 | 1 | 2 | 3 |
| f(x) = x2 | 9 | 4 | 1 | 0'25 | 0 | 0'25 | 1 | 4 | 9 |

Esta curva simétrica se llama parábola.
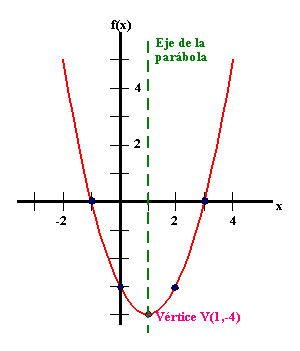
Funciones cuadráticas más complejas se dibujan de la misma forma.
Dibujemos la gráfica de f(x) = x2 -2 x - 3.
| x | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0 | -3 | -4 | -3 | 0 | 5 |
Completando la gráfica obtengo:
Actividades resueltas
Dada la parábola y = x2 - 4 x + 3, determina con precisión las coordenadas de los puntos de la figura:
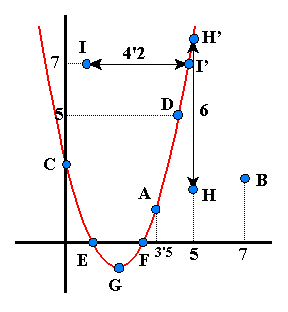
a. Del punto A(x,y) conocemos que x = 3'5. Como A es un punto de la parábola, sus coordenadas cumplirán la ecuación, es decir, y = 3'5 2 - 4·3'5 + 3 = 1'25. Por tanto, A = (3'5,1'25).
b. Del punto B(x,y) conocemos que x = 7. Como B no pertenece a la parábola, no disponemos de ninguna relación que nos permita deducir y en función de x: no es posible conocer con precisión las coordenadas de B.
c. El punto C(x,y) está situado sobre el eje de ordenadas, luego x = 0. Como también es un punto de la parábola, verificará y = 02 - 4·0 + 3 = 3 .Luego C = (0,3).
d. D = (x,5) pertenece a la parábola. Sustituyendo y por 5 en la ecuación de la parábola:
![]() ,
que nos proporciona las soluciones aproximadas x = -0'45 y x = 4'45 .
Observando la gráfica se concluye que el valor adecuado es el segundo (¿por
qué?). Luego D = (4'45,5).
,
que nos proporciona las soluciones aproximadas x = -0'45 y x = 4'45 .
Observando la gráfica se concluye que el valor adecuado es el segundo (¿por
qué?). Luego D = (4'45,5).
e. Los puntos E y F pertenecen al eje OX . Sus coordenadas serán de la forma (x,0) y por ser de la parábola verificarán la ecuación de 2º grado x2 - 4x + 3 = 0 , cuyas soluciones son x = 1 y x = 3. Por tanto, los puntos serán E = (1,0) y F = (3,0).
f. Por la forma simétrica
de la parábola, la abscisa de G = (x,y) es el punto medio del segmento
![]() , es decir,
, es decir,
![]() .
Sustituyendo este valor en la ecuación de la parábola, obtenemos su segunda
coordenada y = 22 - 4·2 + 3 = 4 - 8 + 3 = -1. Luego G = (2,-1).
.
Sustituyendo este valor en la ecuación de la parábola, obtenemos su segunda
coordenada y = 22 - 4·2 + 3 = 4 - 8 + 3 = -1. Luego G = (2,-1).
g. Calculemos las coordenadas del punto H´(x,y) de la parábola que está "justo encima" de H.
Como x = 5, entonces y = 52 - 4·5 + 3 = 25 - 20 + 3 = 8 , es decir, H´= (5,8). H tiene igual abscisa 5 y su ordenada es 6 unidades menos que H´, por tanto, H = (5,2).
h. Calculamos las
coordenadas del punto I´(x,7) que está en la parábola "justo a la derecha"
de I. Como pertenece a la parábola ,
![]() cuyas soluciones aproximadas son x = -0'88 y x = 4'83. I tiene la misma
ordenada 7 y su abscisa es 4'2 unidades menos que la abscisa de I´, es
decir, I = (0'63,7).
cuyas soluciones aproximadas son x = -0'88 y x = 4'83. I tiene la misma
ordenada 7 y su abscisa es 4'2 unidades menos que la abscisa de I´, es
decir, I = (0'63,7).
Determina, por este orden, las coordenadas de los puntos A, B, el vértice V y el punto C de la parábola
y = x2 - x + 1 .
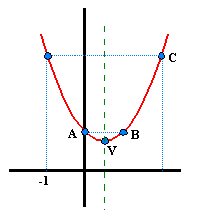
a. A está situado en el eje Y, es decir sus coordenadas son de la forma A(0,y). Puesto que A pertenece a la parábola, y = 02- 0 + 1, y = 1. Luego A = (0,1).
b. B ha de ser de la forma (x,1), por tanto, 1 = x2 - x + 1; 0 = x2- x, 0 = x · (x - 1) de soluciones x = 0 y x = 1. Luego B = (1,1).
c. La 1ª coordenada del
vértice está situada en el punto medio del segmento de extremos 0 y 1, es
decir,
![]() .
La 2ª coordenada se obtiene con la ecuación y = (0'5)2- 0'5 + 1 =
0'75. Las coordenadas del vértice serán V = (0'5,0'75).
.
La 2ª coordenada se obtiene con la ecuación y = (0'5)2- 0'5 + 1 =
0'75. Las coordenadas del vértice serán V = (0'5,0'75).
d. Utilizando la simetría de la parábola puedo calcular la 1ª coordenada de C, x = 2. Por lo tanto,
y = 22-2+1=3. C = (2,3).
Este método se puede generalizar a cualquier parábola de ecuación y = ax2 + bx + c y nos permitirá hallar el vértice de forma inmediata.