1![]()
![]()
![]()
![]()
![]()
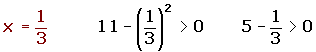
2![]()
![]()
![]()
3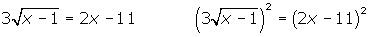
![]()
4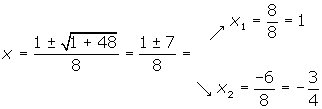
![]()
![]()
![]()
5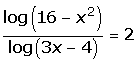
![]()
![]()
![]()
FÓRMULA GENERAL: la incógnita aparece dentro de un/os logaritmo/s
ejemplo: log(x+6) = 1 + log(x-3)
El logaritmo que suele aparecer en las ecuaciones logarítmicas es el decimal o el neperiano y, normalmente, siempre la misma base en toda la ecuación
1) Utilizando las propiedades de los logaritmos, llevar la ecuación a:
log ( ) = número
log ( ) = log ( )
2) Exponenciar en la base de los logaritmos en ambos miembros y llegar a una ecuación polinómica
3) Rechazar las soluciones no válidas (variable de logaritmo menor o igual a 0 )
|
Siempre a partir de la deficición de logaritmo de un número (b) en una cierta base (a): logb(a)=n de forma que bn=a., se deducen las propiedades de los logarítmos. Destacamos aquí las más importantes para resolver las ecuaciones logarítmicas. log A + log B = log (A·B) (permite agrupar en un sólo término una suma de logaritmos) log A - log B = log(A/B) (permita grupar en un sólo término una diferencia de logarítmos) n·log A = log An. (que se usará si es necesario antes que las dos anteriores). En este caso téngase en cuanta que si "n" es un número fraccionario, dentro del log quedará una raiz. n = log 10n (y en particular: "0 = log 1"; 1 = log 10 ) Usando estas propiedades se suelen resolver las ecuaciones logarítmicas más frecuentes. |
EJEMPLOS
1![]()
![]()
![]()
![]()
![]()
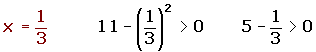
2![]()
![]()
![]()
3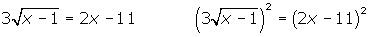
![]()
4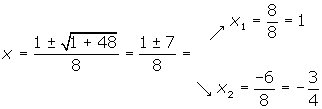
![]()
![]()
![]()
5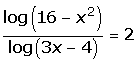
![]()
![]()
![]()