P(x) = 2x4 + x3 − 8x2 − x + 6
Dividimos por Ruffini.
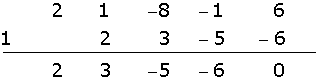
Por ser la división exacta, D = d · c
(x −1) · (2x3 + 3x2 − 5x − 6) = 0
Una raíz es x = 1 .
Continuamos realizando las mismas operaciones al segundo factor.
Volvemos a probar por 1 porque el primer factor podría estar elevado al cuadrado.
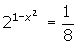
(x −1) · (x +1) · (2x2 +x −6) = 0
Otra raíz es x = -1 .
El tercer factor lo podemos encontrar aplicando la ecuación de 2º grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
![]()
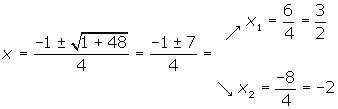
Las soluciones son: x = 1, x = − 1, x = −2 y x = 3/2
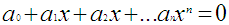 ;
con
;
con