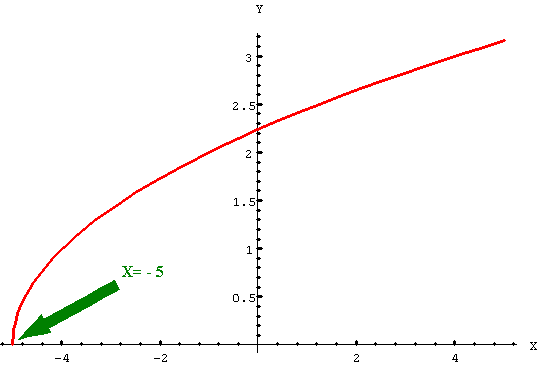
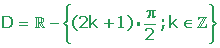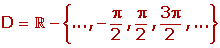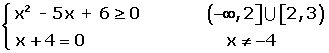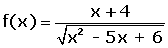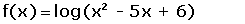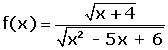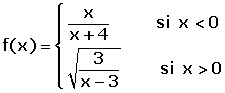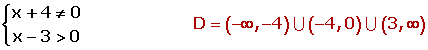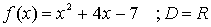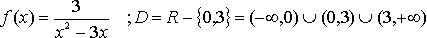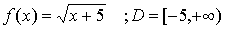bibliografía

En la función que tiene por expresión algebraica y = 2x +1 podemos dar a la variable x el valor que queramos y con ello obtener un correspondiente valor de y. Decimos que en este caso dicha función está definida en todo R (conjunto de los números reales) o bien que su dominio de definición es R.
Sin embargo la función y = 1/x no permite calcular el correspondiente valor de y para todos los valores de x. En este caso el valor x=0 no puede ser del dominio de la función.

Se llama dominio de definición de una función f, y se designa por Dom f, al conjunto de valores de x para los cuales existe la función, es decir, para los cuales podemos calcular y = f(x). El dominio de una función está formado por todos los elementos que tienen imagen.

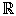D = {x / f (x)}

POLINÓMICAS	El dominio de una función polinómica es
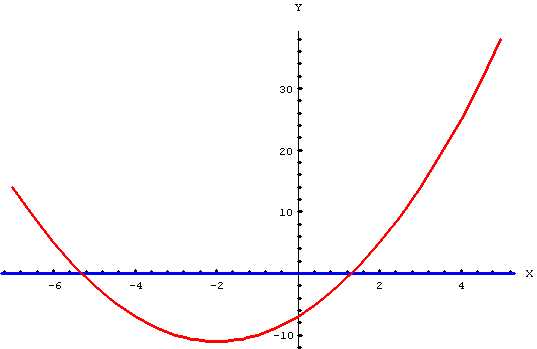
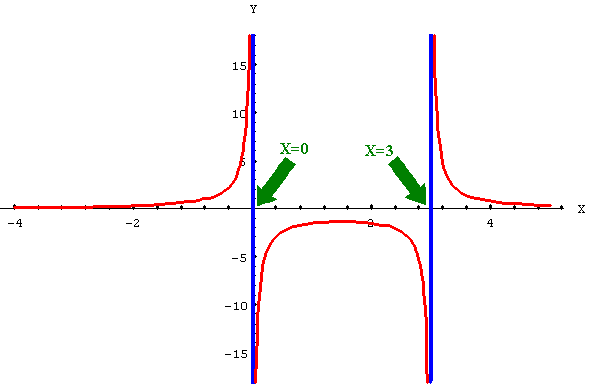
RACIONAL	El dominio es 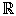menos los valores que anulan al denominador.
IRRACIONAL	El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
EXPONENCIALES	El dominio de las exponenciales se corresponde con el dominio del exponente
LOGARÍTMICAS	El dominio está formado por excepto los números negativos y cero
TRIGONOMÉTRICAS	SENO: El dominio se corresponde con el dominio de aquello sobre lo que se está aplicando el seno. COSENO: El dominio se corresponde con el dominio de aquello sobre lo que se está aplicando el coseno. TANGENTE: (es decir está formado por excepto por π/2 y todas las medias vueltas-kπ-desde el punto π/2, no hay DOMINIO cuando el coseno es 0)
A TROZOS	Se estudia el dominio de cada intervalo indicado, excluyendo los puntos que no estén en ese dominio (concreto del intervalo), pero que pertenezcan al intervalo estudiado. Si en el dominio del intervalo estudiado no están puntos que tampoco están en el intervalo, NO se tienen en cuenta para el dominio final. Dominio final: según lo indicado antes, se suman los dominios de los distintos intervalos