FUNCIONES logarítmicas

 

  • Se llaman funciones logarítmicas a las funciones de la forma f(x) = loga(x) donde "a" es constante (un número) y se denomina la base del logaritmo.

 

  • La función logarítmica que más se utiliza en matemáticas es la función "logaritmo neperiano" y se simboliza normalmente como ln (x), (la función logaritmo en base 10 se simboliza normalmente como log(x)).

 

TRANSLACIONES

 

HORIZONTAL (q=OY)

 

  

f(x) = Ln (x-q)

 
 

VERTICAL (k=OX)

 

  

f(x) = Ln (x) + k

 
 

OBLICUA

 

  

f(x) = Ln (x-q) + k

 

 

 

RECUERDO SOBRE LOGARITMOS

Seguramente ya se han estudiado los logaritmos por lo que conoces la deficición de logaritmo de un número (b) en una cierta base (a): loga(b)=n si se cumple que an=b.

Definíamos por tanto el logaritmo en una cierta base "b" de un número "a" como el exponente al que hay que elevar la base b para obtener el número a.

Esto nos relaciona la función logarítmica con la exponencial. También lo veremos posteriormente de forma gráfica.

También sabremos que la base (b) de los logarítmos debe ser un número positivo (al igual que la base de la potencia de una función exponencial) y además no debe ser 1 ya que log1(a) en general no existe ya que si a no es 1 1n no puede ser a.

Sabemos también que las bases más utilizadas para los logaritmos son las base 10 (logaritmos decimales) y la base el número "e=2,718281.." (logaritmos neperianos).

 

 

 

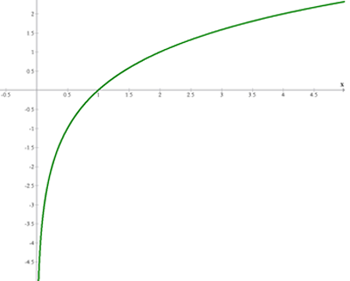
Representación

log

Representación