¿cómo se pueden presentar?

  Tanto en un contexto matemático, como en la vida cotidiana, nos encontramos a menudo con funciones. Se nos presentan de diferentes maneras:
 

1.Mediante su representación gráfica.

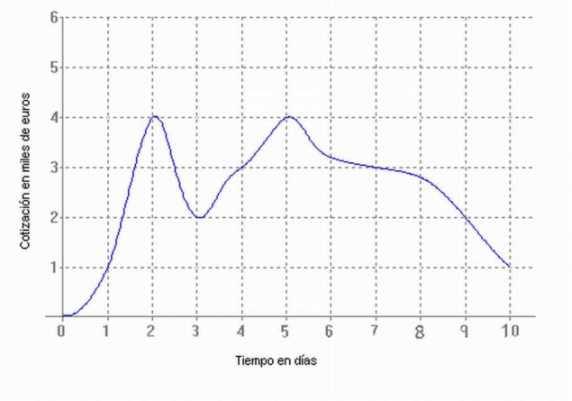
La cotización en bolsa de un determinado producto en los primeros 10 días en que se sacó a bolsa es la función representada en la imagen anterior.  Como mejor podemos apreciar el comportamiento global de una función es mediante su representación gráfica, por eso, siempre nos será de mucha utilidad conseguir representar la función si no nos la dan ya representada. La variable independiente sería el tiempo en días y la variable dependiente el valor de cotización del producto en miles de euros.

2.Mediante una tabla de valores.

 Observa los siguientes datos que se dan en una tabla:
 

 Corresponden al número aproximado de bacterias, en miles, de una colonia a lo largo del tiempo medido en horas.
 La variable independiente es el tiempo medido en horas y la dependiente el número de bacterias en miles.
 Los datos recogidos en esta tabla podrían representarse en un sistema cartesiano y con ello conseguir, al menos de forma aproximada, la gráfica de la función que mide los miles de bacterias en cada hora.
 

3.Mediante su expresión analítica o fórmula.

  El área de un círculo es función de su radio y se calcula a través de la expresión 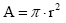. La variable independiente es la medida del radio (aquí se usa la letra r para esta variable) y la dependiente es la medida del correspondiente área que aquí se representa por la letra A.
 La expresión analítica es la forma más precisa y manejable de dar una función, pero a partir de ella el estudio posterior y la obtención de la gráfica es una tarea minuciosa si se quiere obtener una gráfica lo suficientemente real de la función. Siempre es posible dar a la variable independiente valores y conseguir los correspondientes de la variable dependiente con los que construir una tabla y conseguir una gráfica aproximada. Muchas fórmulas son expresiones de ECUACIONES (pincha AQUÍ para acceder a una página web de ecuaciones)
 

4.Mediante un enunciado.

"Un padre que estuvo observando desde el balcón a su hijo Alberto como iba al colegio:  .-De casa salió a las 8.30 y fue seguidito hasta casa de su amigo Tomás. Lo esperó un rato sentado en el banco y luego se fueron juntos, muy despacio, hacia el colegio. Cuando ya estaban llegando, mi hijo se dió cuenta de que se había dejado la cartera en el banco; volvió corriendo, la recogió y llegó a la escuela a las 9 en punto."    Este enunciado representa una función que describe la distancia a la que se encuentra Alberto según el instante entre las 8.30 y las 9.00 de la mañana, y su gráfica aproximada es la representada a la derecha.
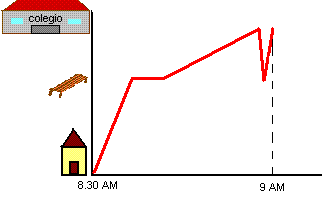
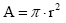