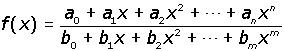-
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:
![]() .
.
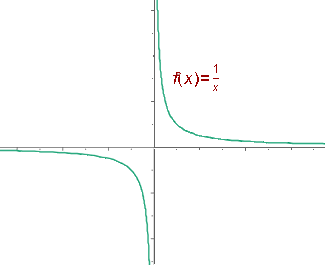
Sus gráficas son hipérbolas.
-
También son hipérbolas las gráficas de las funciones.
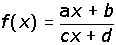
, que transformaremos en
hipérbolas
![]() que son las más sencillas de representar.
que son las más sencillas de representar.
Sus asítontas son los ejes.
El centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.
![]()
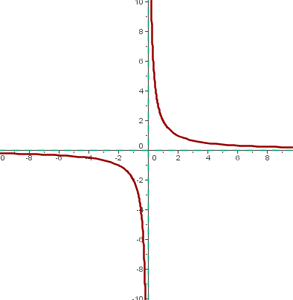
A partir de estas hipérbolas se obtienen otras por traslación.
1. Traslación vertical
![]()
El centro de la hipérbola es: (0, a).
Si
a>0,
![]() se desplaza hacia arriba
a
unidades.
se desplaza hacia arriba
a
unidades.
![]()
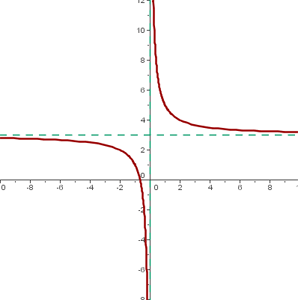
El centro de la hipérbola es: (0, 3)
Si
a<0,
![]() se desplaza hacia abajo
a
unidades.
se desplaza hacia abajo
a
unidades.
![]()
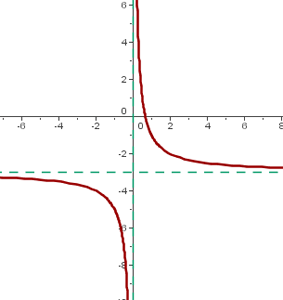
El centro de la hipérbola es: (0, -3)
2. Traslación horizontal
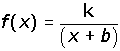
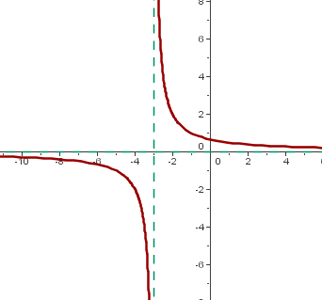
El centro de la hipérbola es: (-b, 0).
Si
b> 0,
![]() se desplaza a la izquierda
b
unidades.
se desplaza a la izquierda
b
unidades.
![]()
El centro de la hipérbola es: (-3, 0)
Si
b<0,
![]() se desplaza a la derecha
b
unidades.
se desplaza a la derecha
b
unidades.
![]()

El centro de la hipérbola es: (3, 0)
3. Traslación oblicua
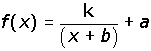
El centro de la hipérbola es: (-b, a)
![]()
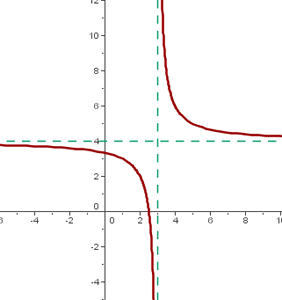
El centro de la hipérbola es: (3, 4).
NOTA: Para representar hipérbolas del tipo:
![]()
se divide (pincha AQUÍ para recordar cómo se dividen polinomios) y se escribe como:
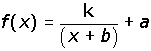
Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a los ejes.
![]()
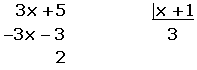
![]()
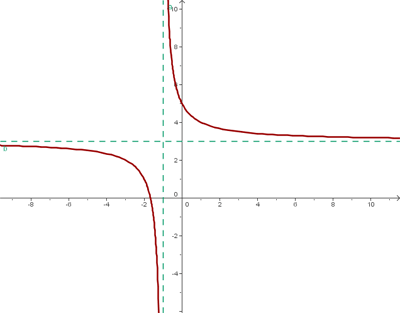
El centro de la hipérbola es: (-1, 3).