Definición de función

Una función es una relación entre dos variables a las que, en general, llamaremos x e y.

x es la variable independiente
y es la variable dependiente

La función asocia a cada valor de x un único valor de y. Se dice que y es función de x, lo que se escribe

y = f (x)

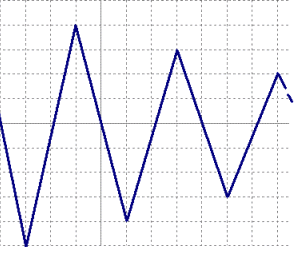
Sobre unos ejes cartesianos representamos las dos variables:
La x sobre el eje horizontal (eje de abscisas).
La y sobre el eje vertical (eje de ordenadas).
Cada punto de la gráfica tiene dos coordenadas, la abscisa x y la ordenada y.
El tramo de valores de x para los cuales hay valores de y se llama dominio de definición de la función.
Los ejes deben estar graduados con las correspondientes escalas para que puedan cuantificarse los valores de las dos variables.

La noción actual de función comienza a gestarse en el siglo XIV, cuando empiezan a preocuparse de medir y representar las variaciones de ciertas magnitudes, como la velocidad de un cuerpo en movimiento. El nombre de función proviene de Leibnitz. A partir de los siglos XVIII y XIX el concepto de función se hace el eje central de las matemáticas, su estudio a través del cálculo y sobre todo de las ecuaciones diferenciales se hace totalmente indispensable para llevar adelante todo el desarrollo científico y tecnológico, primero al servicio de la Física y luego de otros campos.

¿Cómo se nos presentan?

Tanto en un contexto matemático, como en la vida cotidiana, nos encontramos a menudo con funciones. Se nos presentan de diferentes maneras:

1. Mediante su representación gráfica.

2. Mediante una tabla de valores.

3. Mediante su expresión analítica o fórmula.

4. Mediante un enunciado.

Pincha AQUÍ para ampliar

Aplicaciones de las funciones reales

Generalmente se hace uso de las funciones reales, (aún cuando el ser humano no se da cuenta), en el manejo de cifras numéricas en correspondencia con otra, debido a que se está usando subconjuntos de los números reales. Las funciones son de mucho valor y utilidad para resolver problemas de la vida diaria, problemas de finanzas, de economía, de estadística...(sigue leyendo AQUÍ)

¿Qué es el dominio de una función?

En la función que tiene por expresión algebraica y = 2x +1 podemos dar a la variable x el valor que queramos y con ello obtener un correspondiente valor de y. Decimos que en este caso dicha función está definida en todo R (conjunto de los números reales) o bien que su dominio de definición es R.
Sin embargo la función y = 1/x no permite calcular el correspondiente valor de y para todos los valores de x. En este caso el valor x=0 no puede ser del...(Pincha AQUÍ para ampliar)

¿Cuándo una gráfica no corresponde a una función?

De las dos gráficas que se muestran a continuación, la de la izquierda corresponde a una función y la derecha no. Observa:

En ésta a cada valor de x de la variable independiente (ejede abscisas) le corresponde un único valor imagen y de la variable dependiente (ordenadas).

En ésta hay algunos valores de la variable independiente x a los que corresponden más de un valor de la dependiente , lo que contradice la definición de función.