tienen el denominador irracional. Con frecuencia es
conveniente transformarlas en otras expresiones
equivalentes que tengan el denominador racional, con lo
que se dice que se les ha racionalizado el denominador.
Para ello se siguen distintas estrategias:
En los dos ejemplos anteriores se
ha multiplicado un denominador del tipo
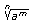por
otro radical del mismo índice,
,
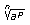y tal que el producto de sus bases am,
ap, sea una potencia de an.
En consecuencia, ha habido que multiplicar el numerador
por la misma expresión.
En los dos ejemplos anteriores se
ha utilizado la identidad (a + b)(a – b)
= a2 – b2 para hacer
desaparecer las raíces cuadradas del denominador
multiplicándolo por la expresión correspondiente que,
por tanto, también ha multiplicado al numerador.
Ejercicios: expresar un
radical en forma de potencia
6.-
Racionalización de denominadores
por
otro radical del mismo índice,
,
y tal que el producto de sus bases am,
ap, sea una potencia de an.
En consecuencia, ha habido que multiplicar el numerador
por la misma expresión. 