|
||||||||||||
|
| DADOS |
La teoría de la probabilidad está muy relacionada con los juegos de azar como el lanzamiento de dados. Antes de participar en cualquiera de estos juegos es conveniente saber cuál es la probabilidad de que salga un resultado u otro.
| Probabilidad en los lanzamientos |
Si
lanzamos un solo dado, existe la misma probabilidad de que salga cualquiera de
los seis números, es decir, es tan probable que salga
1 como
que salga
2 o
3 o
4 o
5 o
6.
Esta probabilidad es
![]() .
.
Al lanzar dos dados, decimos que el número que cae es la suma de los números que aparecen en las caras de ambos dados. Por ejemplo, si en uno de los dados hay un 2 y en el otro un 4, decimos que cayó un seis. Cuando lanzas dos dados no todos los números tienen la misma probabilidad de caer. Veamos cuáles son los números que pueden caer y cómo podrían obtenerse. Para no confundirnos con lo que sale en cada dado, imaginemos que cada uno de los dados tiene un color diferente y que el color del número corresponde al color de lado en que salió. Supongamos que uno de los dados es rojo y el otro es azul.
Fíjate en la siguiente tabla. En la columna de la izquierda hemos colocado las sumas que puedes obtener al lanzar dos dados. En la columna de la derecha está el número de maneras de obtener esas sumas. Por ejemplo, el 2 sólo puede salir de una manera: que en ambos dados salga un 1 (1+1); pero hay dos maneras de que salga un 3: que en el dado rojo salga 1 y en el azul salga un 2 o que en el rojo salga un 2 y en el azul salga un 1 ( 1 + 2 y 2 + 1 ). Llena la columna del centro con las diferentes maneras de obtener cada una de las sumas.
|
suma
|
manera
de obtenerla |
total
|
|
2
|
1
+ 1
|
1
|
|
3
|
1
+ 2 |
2
|
|
4
|
1+3
3+1
2+2
|
3
|
|
5
|
1+4
4+1
2+3
3+2
|
4
|
|
6
|
1+5
5+1
3+3
4+2
2+4
|
5
|
|
7
|
3+4
4+3
3+5
5+2
6+1
1+6
|
6
|
|
8
|
4+4
3+5
5+3
2+6
6+2
|
5
|
|
9
|
6+3
3+6
5+4
4+5
|
4
|
|
10
|
5+5
6+4
4+6
|
3
|
|
11
|
5+6
6+5
|
2
|
|
12
|
6+6
|
1
|
En esta gráfica se muestra la comparación del número de maneras de obtener cada uno de los números.

Como puedes ver, tendrías más probabilidad de ganar si le apuestas al 7 porque hay más formas de obtener 7 que de obtener cualquier otro número.
¿Qué crees que pase si lanzas 3 dados? ¿Habrá algún número que tenga más probabilidades que otro? Por supuesto!!
Ésta es la gráfica del total de formas de obtener los diferentes números.
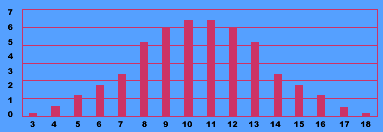
Y a partir de 3 lanzamientos la gráfica que muestra la probabilidad de obtener cada suma de números siempre tiene una forma parecida a las dos gráficas anteriores.
| Muy curioso: |
-El tratamiento teórico de los problemas de combinatoria y probabilidad se inicia en el siglo XVII con los matemáticos Blaise Pascal (1623-1662) y Pierre de Fermat (1601-1665).
El problema que dio origen a la teoría tiene que ver con la división de las apuestas en un juego de lanzamiento de monedas que el Caballero de Meré –un jugador empedernido– le planteara a Blaise Pascal.
El juego consistía en el lanzamiento de una moneda sucesivas veces. El ganador es el jugador que alcanza primero 6 éxitos (6 caras ó 6 números). Pero el juego se interrumpe si en el noveno lanzamiento se obtiene el resultado 5 a 4.
El problema planteado por el Caballero de Meré tenía que ver con la forma en que se deben repartir las apuestas acumuladas al interrumpirse el juego, en tanto no hay un ganador. El Caballero de Meré creía que lo más justo era repartir las apuestas en la relación 5 a 4, pero no estaba convencido. Pascal demostró que las apuestas debían repartirse en la relación 3 a 1 si se toma en consideración que, de continuar el juego, quien lleva 5 éxitos tiene 3 veces más posibilidad de ganar el juego que su contrincante.
-En el enlace podrás comprobar mediante tiradas de dados la Ley de los Grandes Números, primer teorema de probabilidad, que establece que la frecuencia de los resultados de un cierto experimento aleatorio, tienden a estabilizarse en cierto número, que es precisamente la probabilidad, cuando el experimento se realiza muchas veces.
http://www.eustat.es/eskola/dados.asp?idioma=c
